Election 2017 guide: What is swing, how is it calculated and why is it important?

One of my most prized possessions is a first edition of The British General Election of 1945, the first in the Nuffield general election series. Appendix III of the volume is entitled “The Relation of Seats to Votes” and comprises 16 pages and ten diagrams (that would almost certainly reduce our colleagues in Visual Journalism to tears) and was written by a Mr DE Butler of New College, Oxford, who was all of 23 years old at the time of publication. This Appendix created the concept of swing that we have used ever since:
“It is intended in this appendix to demonstrate that now…the membership of a new House of Commons can be foretold within reasonable limits….In the course of the argument it will be shown how, since the workings of the electoral system are in large measure predictable, it is possible to indicate graphically the swing in popular opinion necessary to oust a majority government…The aim of this is to show the number of seats which would, all other things being equal, change hands as a result of a given swing in popular votes.”
But how does swing work in practice? In his invaluable book Brewer’s Politics (published by Cassell) Nicholas Comfort describes swing in the following terms:
“The statistical measure by which the switch of voters from one party to another on a national or constituency basis can be judged. It is calculated by adding the rise in one party’s vote to the fall of the other, and dividing by two.”
Let us look at a few practical examples of how swing is calculated.
Most national opinion polls deal in complete figures (no decimal points). So, when we are looking at individual opinion polls in a general election we need to know the rounded-up percentage figures for the main parties in the previous general election. On that basis, in 2015’s election there was 38 per cent support for the Conservatives and 31 per cent for Labour (GB not UK figures). If a poll is published giving 46 per cent support for the Conservatives and 27 per cent for Labour we can see that, compared with 2015’s election, that represents +8 for the Conservatives and -4 for Labour. You add these two figures together and that makes 12 and then divide by two which makes 6 which means a 6 per cent swing from Labour to Conservative since 2015.
How do we calculate swings in parliamentary constituencies?
Let us invent a constituency and call it Yellow Town Central. The table below sets out the results in 2015 and in the 2017 general election in this constituency.
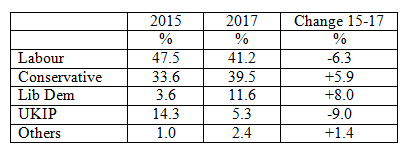
In order to calculate the swing between 2015 and 2017, we add -6.3 to +5.9 which makes 12.2, then divide this by 2 which gives us a swing of 6.1 per cent from Labour to Conservative.
To calculate the swing required for an individual seat to be lost by the incumbent party, we look at the majority of the winning party at the previous election over the second-placed party, say 12.8 per cent, and divide this by two, which gives us 6.4 per cent and that is the minimum swing required for the seat to change hands.
But how do we calculate swing (I hear you ask) in a seat where the shares of the two top parties both increase? Say there was a Lib Dem seat with the Conservatives in second place in 2015 and in 2017 the Lib Dem share went up +8.5 and the Conservative share by +5.3? In this instance we take the smallest increase (5.3) from the largest (8.5) which leaves us 3.2 which we again divide by 2 and the resulting 1.6 per cent is the swing from Conservative to Lib Dem in that seat.
Oh! The joys of psephology.
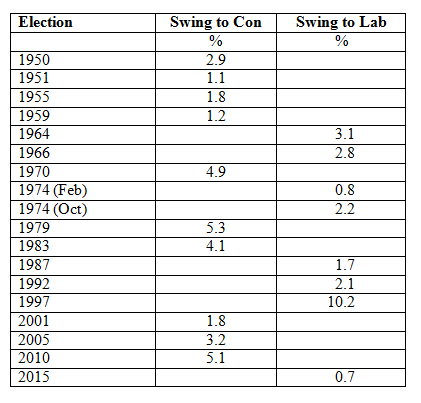
The table below sets out the national swings for every postwar general election.
Conservative-Labour swings at general elections (based on voting in Great Britain only)
David Cowling is a political analyst and Senior Visiting Fellow at King's College London. He will be commenting on the election for The Independent throughout the campaign

 Yahoo News
Yahoo News 
